ベイズ推定とグラフィカルモデルの略解をまとめています。あくまで個人のメモですので、必ずしも正しい保証はありません。もしミスがある場合は教えていただければ幸いです。今回はSection10です。

1. 無向グラフィカルモデルの分配関数と因子グラフ

$\{x_i\}_{i=1}^4\in\{0,1\}\\ \displaystyle P(x_1,x_2,x_3,x_4)=\frac{1}{Z}\phi(x_1,x_2,x_3)\phi(x_2,x_3,x_4)\\ \phi(0,0,0)=3,\quad \phi(0,0,1)=1,\quad \phi(0,1,0)=1,\quad \phi(0,1,1)=2\\ \phi(1,0,0)=1,\quad \phi(1,0,1)=2,\quad \phi(1,1,0)=2,\quad \phi(1,1,1)=3\\$

とする。このとき、分解関数 $Z$ は、

$3*3+3*1+1*1+1*2+1*1+1*2+2*2+2*3+\\ 1*3+1*1+2*1+2*2+2*1+2*2+3*2+3*3=59$

対応する因子グラフは、

f:id:hiden-cubist:20190122174827p:plain

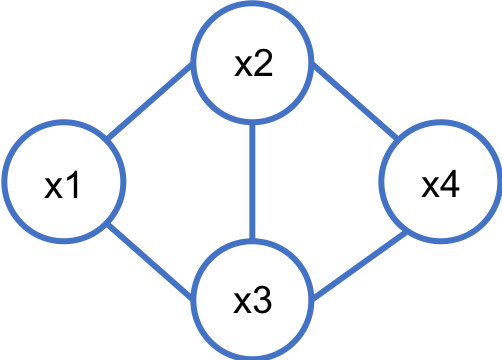
2. 離散同時分布の要素の数

$\{x_i\}_{i=1}^6\in\{1,\cdots,5\}\\ P(x_1,\cdots,x_6)=P(x_1|x_2)P(x_2|x_3,x_4)P(x_3)P(x_4|x_5)P(x_5)P(x_6)$

右辺の分離を考えた場合、要素数は

$5^2+5^3+5^1+5^2+5^1+5^1=190$

全てが互いに依存している場合、要素数は

$5^6=15625$

対応する因子グラフは、

f:id:hiden-cubist:20190122174933p:plain

3. 混合正規分布のグラフィカルモデル

f:id:hiden-cubist:20190122174943p:plain
xは訓練データ、hは隠れ変数であり、これらがI組ある。また、λはhのカテゴリカル分布のパラメータ、μ、Σはxの正規分布のパラメータであり、K組ある。

4. head-to-tailのグラフィカルモデル

$\begin{align} P(A,B|C) \displaystyle &=\frac{P(A,B,C)}{P(C)}\\ \displaystyle &=\frac{P(A)P(C|A)P(B|C)}{P(C)}\\ &=P(A|C)P(B|C)\\ P(A|B,C) \displaystyle &=\frac{P(A,B|C)}{P(B|C)}\\ \displaystyle &=\frac{P(A|C)P(B|C)}{P(B|C)}\\ &=P(A|C) \end{align}$